|
|
|
 |
|
Given a right line AB, construct a square on a segment of that
line. |
 |
|
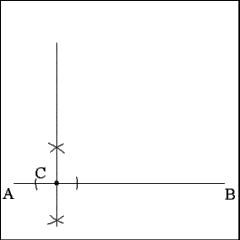
Select any point (C) near one end of Line AB.
Construct a line from Point C that is perpendicular to Line AB
and extend the perpendicular line to a length equal the desired length
of the side of the square. |
 |
|
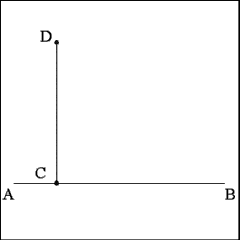
Mark the end of the perpendicular line Point D.
|
 |
|
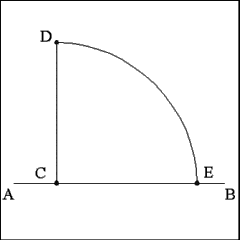
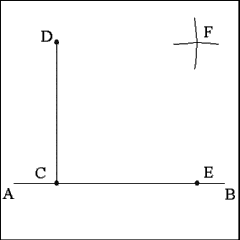
Using Point C as center and opening the compass to a length equal
to the distance between points C and D, describe an arc of a circle from
Point D that cuts Line AB at Point E. Line CD should be equal to Line Segment
CE. |
 |
|
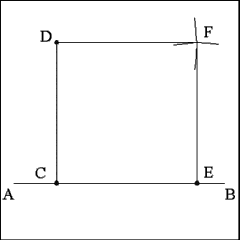
Using Point D as center describe an arc of a circle above Point
E that has a radius equal to the length of Side CD.
Using Point E as center describe a second arc above Point E that
has a radius equal to CE and intersects the preceding arc at Point F. |
 |
|
Produce right lines from Point D to Point F and from Point E to
Point F. These two lines (DF and EF) complete the final two sides of Square
CDFE. |
|
|
|