|
|
|
 |
|
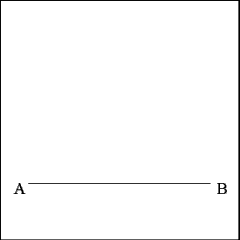
Given a right line AB, construct an equilateral triangle on a
segment of that line. |
 |
|
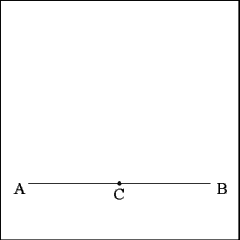
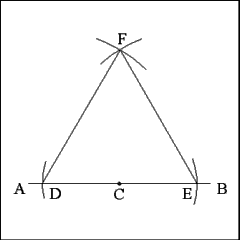
Select any point (C) near the middle of Line AB to begin constructing
an equilateral triangle. |
 |
|
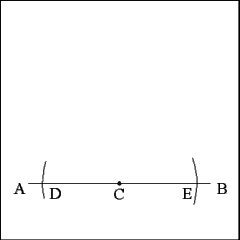
Open the compass to any length and cut Line AB with two arcs,
one on each side of Point C on Line AB. |
 |
|
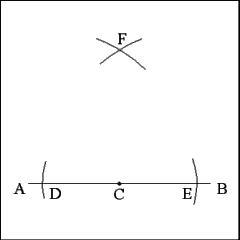
Using points C and D as centers, describe two intersecting arcs
above Point C that have a radius equal to the distance between Points E and
D. The point where these arcs intersect (Point F) will be the vertex of the
equilateral triangle. |
 |
|
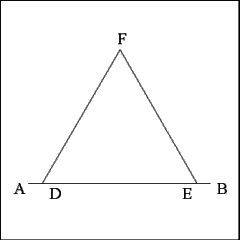
Produce two right lines, one from Point F to Point E and the other
from Point F to Point D. These lines form two sides of the equilateral triangle
CFD. |
 |
|
Triangle DFE is an equilateral triangle: all three sides are the
same length; it is also equiangular: all three angles measure 60 degrees. |
|
|
|