In the course of both drawing and evaluating the defensive characteristics of fortifications perpendiculars are oftimes required at and near the extremities of right lines. Most other perpendicular constructions require a bit of space on either side of the point of construction, but this one takes advantage of the properties of circles and isosceles right triangles to create a perpendicular line working from just one side of the point of construction. Some care must be exercised in the execution of this construction: exact points on the circumference of circles can be difficult to place accurately.

Given a Right Line AB, construct a perpendicular line near one of the extremities of the line, that is, near Point A or Point B.

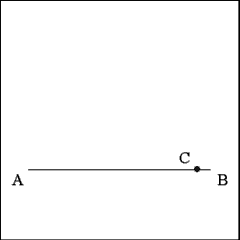
Mark a point (C) on Line AB where the perpendicular should intersect the given Line AB.

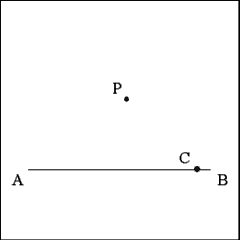
At any point exterior to Line AB mark a second point (P).

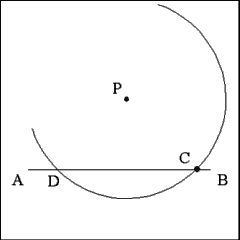
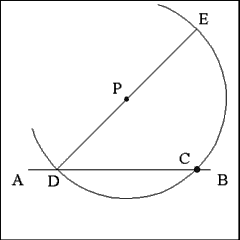
Using Point P as center and opening the compass to a length equal to the distance between points D and C describe an arc that passes through Line AB at Point D and again through Point C, making sure to extend the arc above Point C.

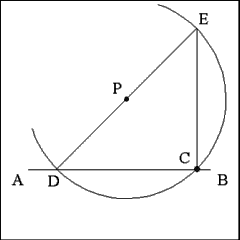
Draw a diameter of the arc from Point D on Line AB through Point P and on to the arc above Point C at Point E.

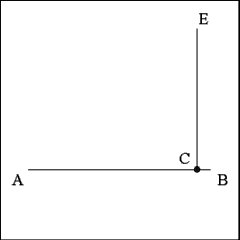
Produce a line from Point C to Point E. This line (CE) will be perpendicular to Line AB.

Note: That the angles EDC and CED measure 45 degrees and lines DC and CE are the same length, making the constructed triangle DCE an isosceles right triangle.

Line CE stands perpendicular to Line AB, even after all the construction lines and marks are erased.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~