|
|
|
 |
|
Given a circle (O) inscribe a square inside the circle. |
 |
|
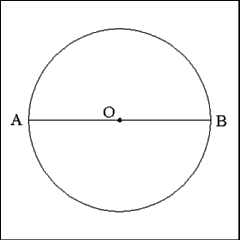
Using a straightedge draw a diameter (AB) through the center (O)
of the circle. |
 |
|
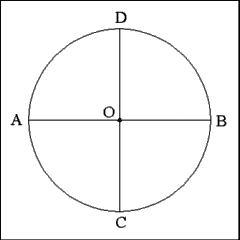
Bisect the diameter AB with a second diameter (CD). It is important
to bisect the first diameter with a second perpendicular diameter to insure
that all the points that intersect the circumference of the circle are the
same distance from the enter of the circle and from each other; equal distances
will define a square rather than produce some other off the wall quadrilateral. |
 |
|
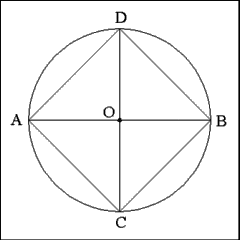
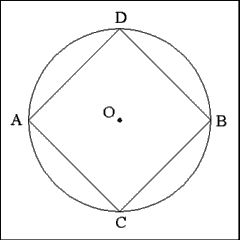
Produce right lines joining the ends of collateral diameters (where
they intersect the circumference of the circle): D to B; B to C; C to A;
A to D. |
 |
|
These connecting lines (DB, BC, CA, AD) form the four sides
of square ACBD inside the circle. |
|
|
|