|
|
|
 |
|
Given a circle inscribe a pentagon inside the circle. |
 |
|
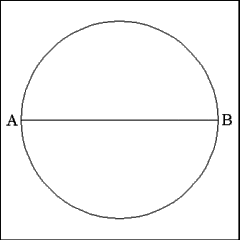
Draw a diameter (AB) through the center of the circle. |
 |
|
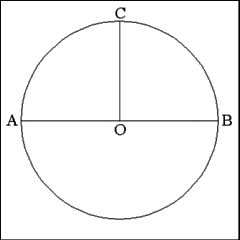
Bisect the diameter (AB) and construct a radius (OC) that is
perpendicular to diameter AB. |
 |
|
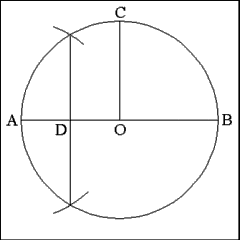
Bisect the radius AO and mark the bisecting point as Point D. |
 |
|
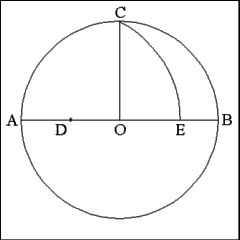
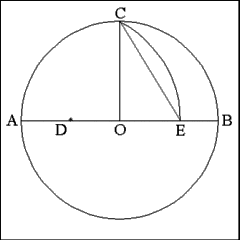
Using Point D as center describe an arc of a circle that has a
radius equal to the distance between Point D and Point C that passes from
Point C to Diameter AB at Point E. |
 |
|
Produce a right line from Point C to Point E. This line (CE) is
approximately equal to the length of each side of the pentagon. |
 |
|
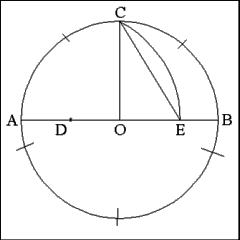
Opening the compass to a length equal to line CE and starting
from any point on the circumference of the circle, successively mark points
along the circumference. These points will be the vertices of the pentagon's
five angles. |
 |
|
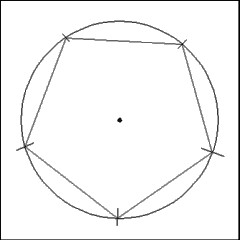
Connect each successive marked point on the circumference of the
circle with right lines. These lines form the five sides of a regular pentagon. |
 |
|
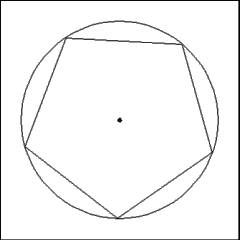
Removing all the construction points and lines leaves a nicely
done regular pentagon inside the original circle. |
|
|
|