|
|
|
 |
|
Given a circle (O) of any diameter inscribe a regular hexagon
inside the circle. |
 |
|
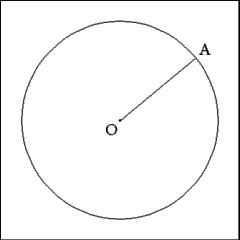
Draw a radius (OA) of the circle. For a regular hexagon the length
of the radius of the circle is equal to the length of the sides of the hexagon. |
 |
|
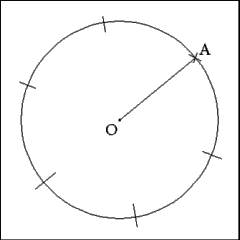
Opening the compass to a length equal to radius OA and starting
from any point (A) on the circumference of the circle, mark successive points
along the circumference of the circle. These points locate the position of
the vertices of the hexagon's angles. |
 |
|
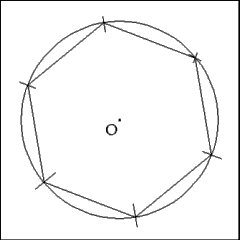
Connect consecutive points along the circumference with right
lines. These lines form the sides of the hexagon. |
 |
|
With all construction marks and line erased this construction
results in a regular hexagon inscribed inside a circle |
|
|
|