This construction comes very close to constructing a regular heptagon inside a circle. The line it uses to locate the vertices of the heptagon's angles along the circumference of the circle is actually not quite long enough; the last side constructed will be slightly longer than the preceding six sides.

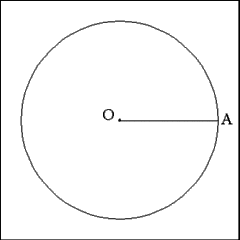
Given a circle (O) of any circumference, inscribe a heptagon inside the circle. Draw a radius (OA) of the circle. This may be accomplished by producing a right line from Point O, the center of the circle, to any point on the circumference of the circle.

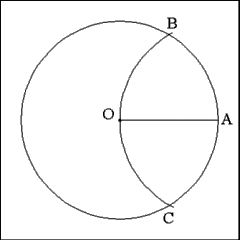
Using Point A as center describe an arc with a radius equal to the radius (OA) of the circle that cuts the circumference of the circle at two points above and below Radius OA at Points B and C.

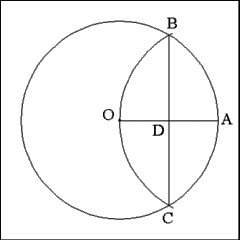
Produce a right line from Point B to Point C that intersects the radius (OA) of the circle at Point D.

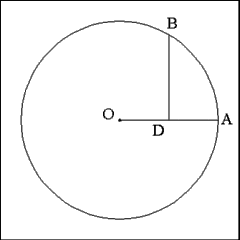
Half of Line BC, Line BD, has a length that is approximately equal to the length of one side of the heptagon.

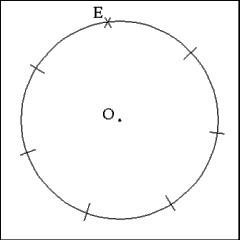
Opening the compass to a length equal to BD and starting at any point (E) on the circumference of the circle, successively mark the points of the heptagon's vertices along the circumference of the circle. As noted, the distance between the first point marked and the last point marked will be slightly longer than the distance between the other points.

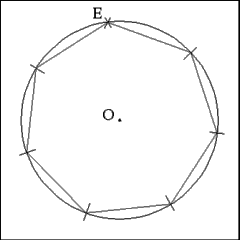
Connect consecutive points along the circumference of the circle with right lines to form the seven sides of the heptagon.

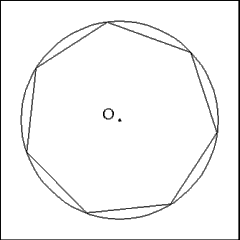
Removing all the construction lines and points reveals a close approximation of a regular heptagon.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~