Given a circle (O) construct a regular octagon inside the circle.

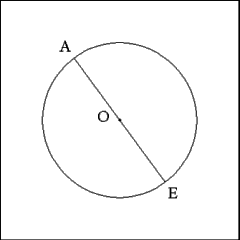
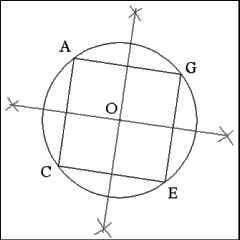
Produce a diameter  (AB) through Circle O.

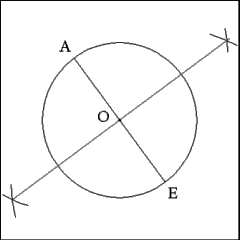
Construct a second diameter that is perpendicular to Diameter AB.

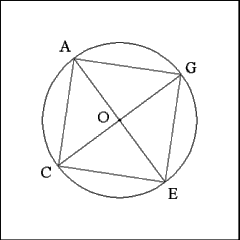
Mark the points where the second perpendicular diameter intersect the circumference of Circle O as Points C and G.

Connect collateral extremities of the diameters (G to A, A to C, C to E, E to G) to construct a square inside Circle O.

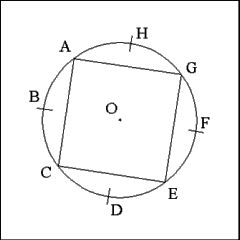
Bisect each side of the square (GA, AC, CE, and EG) and extend the bisecting lines through the circumference of the circle.

Mark the points where the bisecting lines intersect the circumference of Circle O as Points H, B, D, F.

There should be four points marked  points (H, B, D, F) along the circumference and four points where the corners of the inscribed square lie on the circumference of the circle (A, C, E, G). These points mark the vertices of the inscribed octagon's eight angles.

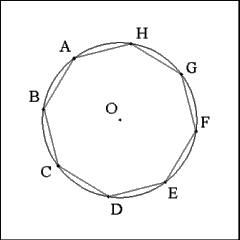
To establish the eight sides of the octagon connect consecutive marked points with right lines ( A to B, B to C, C to D, etc...).

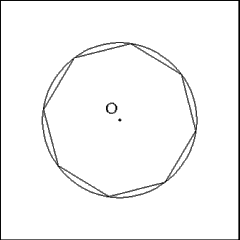
Removing all of the construction lines and markers reveals a regular octagon of an indefinite perimeter and indefinite side lengths.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~