|
|
|
 |
|
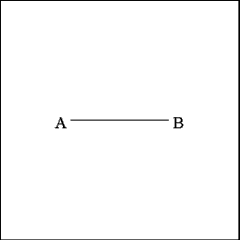
Draw Line AB of any length. |
 |
|
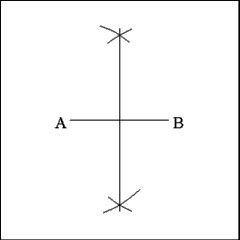
Bisect Line AB; mark the bisecting point as Point C. |
 |
|
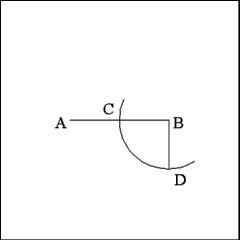
From either end of Line AB construct a line (BD) perpendicular
to Line AB. This perpendicular line should fall on the opposite side of Line
AB from the side on which the pentagon will be constructed. |
 |
|
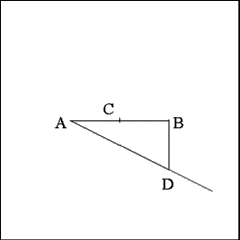
Extend Line BD a distance equal to 1/2 Line AB (that is equal
to line segment to AC or CB). |
 |
|
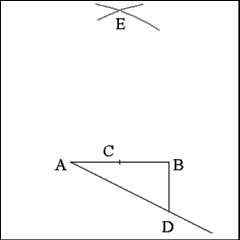
Produce a right line from Point A to Point D and extend this line
a distance equal to 1/2 AB. |
 |
|
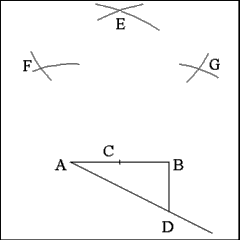
Using Points A and B as centers describe two intersecting arcs
with radii equal to the length of the constructed extension of Line AD. Mark
the intersecting point as Point E. |
 |
|
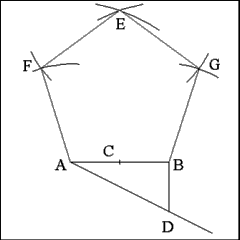
To establish the position of the other two vertices of the polygon's
five angles open the compass to a length equal to the distance between points
A and B (this is the length of one side of the polygon).
Using Points A, B, and E as centers describe arcs that intersect
at points F and G. F and G locate the positions of the vertices of the final
two angles of the polygon. |
 |
|
Connect consecutive vertices with right lines to establish the
sides of the polygon (A to F, F to E, E to G, G to B). |
 |
|
Remove all the construct lines and markers to reveal a regular
polygon with an indefinite perimeter and indefinite length for its sides. |
|
|
|