This fortunate construction provides one the means to draw measured regular pentagons of any desired or required perimeter. For the purpose of providing a clear example it will be claimed that a regular pentagon with a perimeter of 45 inches is very much the object of our immediate attention and obsession and unless we have one we simply will not be able to scroll all the way to the bottom of this happy page. It makes a good beginning to find out how long each side of the pentagon must be. This rudimentary dimension is easily found by dividing the length of the perimeter by the number of sides, or, in this case, 45 by 5. This gives a quotient of 9; and so each side of our regular pentagon must needs be 9 inches long.

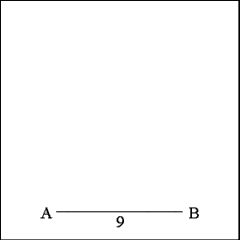
Draw a measured line (AB) that is equal to length of one side of the pentagon. As already noted, each side of a regular pentagon with a perimeter of 45 inches must be 9 inches long.

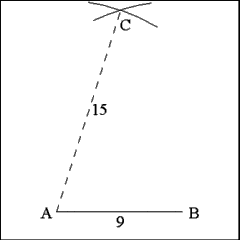
Having previously accomplished a rather easily done thing it will next be necessary to find the position of the vertex of the angle that is opposite to Side AB. This requires a hasty resort to the mystical hand of geometrical proportions: open the compass to a length that is equal to one-third (1/3) the perimeter of the pentagon, a length that is discovered, in a very calculating and mathematical way, by multiplying 45 by 1/3 (or, as one's abilities  may flow, by dividing 45 by 3). This gives a necessary length of 15 inches. Using each end of the measured side of the pentagon (Points A and B) as centers describe two arcs of circles with radii of 15 inches that will intersect at point C. Point C is the discovered vertex of the angle of the pentagon opposite to Side AB.

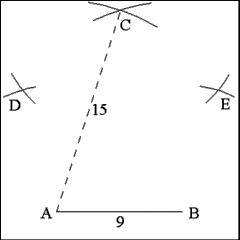
Having found the extremities of one side of the pentagon (Points A and B, which are, by necessity, the vertices of two of the pentagon's angles) and the vertex of their opposite angle (C) the vertices of the pentagon's angles that fall between them may be found. Begin by opening the compass to a length equal to one side of the pentagon (9 inches in this case); using B as center describe an arc that seems a likely spot for the angle that will fall between B and C. Then use C as a center and repeat that procedure; mark the point where the two arcs intersect as Point E. Point E is the vertex of the angle that falls between the vertices C and B. Do the same for the other angle that falls between Points C and A to find Point D.

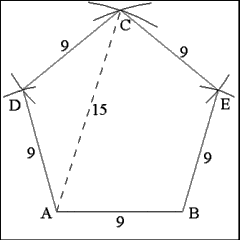
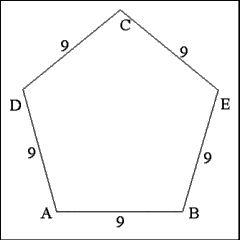
Produce right lines that join consecutive angle vertices: A to D, D to C, C to E, E to B. These lines form the other four sides of the pentagon.

Removing construction lines and marks reveals a well formed regular pentagon in which all sides are equal to 9 inches and the perimeter is equal to 45 inches.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~