This example constructs a regular hexagon with a perimeter of 30 inches and sides 5 inches long.

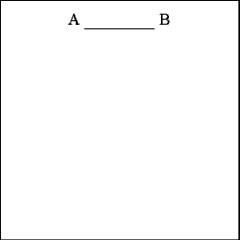
Draw a right line (AB) that is equal in length to one side of the hexagon, in this case each side will be 5 inches long ( 30 / 6 = 5).

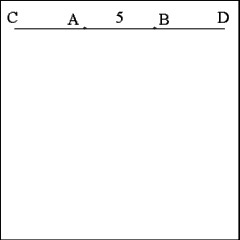
Extend the length of Line AB a distance equal to three times its own length; this increase can be produced from one or the other end of Line AB, or from both ends of Line AB, as was done here, to Points C and D.

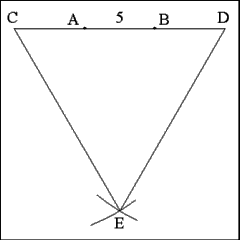
Construct an equilateral triangle using the distance from Point C to Point D as the length of the sides of the triangle.

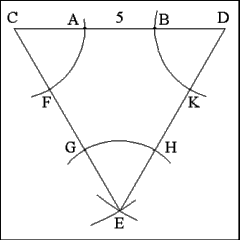
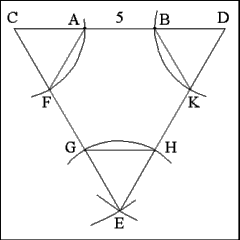
Trisect each side of the triangle. To do this open the compass to a distance equal to the length of Line AB; using each angle of the triangle (C, D, E) as center, cut adjacent sides by a single arc (from E, describe an arc that cuts sides EC and ED at points G and H, etc...).

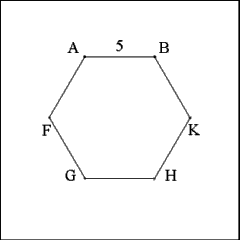
Join consecutive arc points along the perimeter of the triangle (A to F, F to G, G to H, etc...) with right lines.

Removing all of the construction lines and points reveals a regular hexagon with sides 5 inches long and a perimeter of 30 inches.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~