It is very useful in drawing fortifications to be able to control the dimensions of the various polygons that must necessarily be created to represent the outlines or sundry elements of fortifications. This construction allows one to create a regular octagon when the perimeter of the polygon is already known: it is quite a common thing when drawing field fortifications to first perform all the requisite calculations to determine the development of the parapet required for a garrison and its armament and only after to select a particular regular or irregular trace. Knowing the development of the interior crest of the parapet and having selected a regular octagon as the trace, this construction can be used to actually begin drawing a design for the required field fortification.

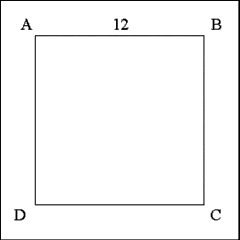
Construct a square with sides that are equal to three-tenths (3/10) the perimeter of the desired octagon. In this case the perimeter of the octagon will be 40 inches; 3/10 of 40 is 12 inches so each side of this square will be 12 inches long.

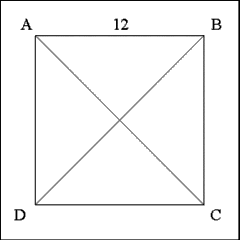
Using a straightedge produce two diagonals from A to C and B to D.

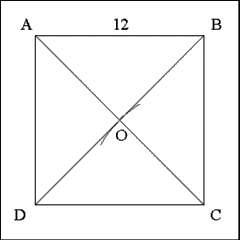
Using any angle of the square as center, in this case C, describe an arc that is equal to one half the length of the diagonal of the square, measured from C to O.

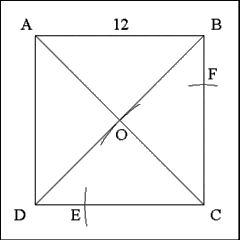
Keeping the compass open to the half-diagonal distance, and successively using each angle vertex as a center, cut adjacent sides of the square with small arcs of circles. Here the arcs are centered on Point C and cut sides CB at F and side CD at E. Repeat this step from each of the three remaining corners.

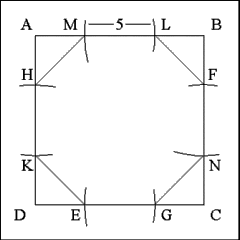
Produce right lines that cut off each corner of the square; that is draw lines from L to F, N to G, E to K, and H to M. These line form four sides of the octagon. The central trisections on each side (FN, GE, KH, and ML) form the other four sides of the octagon.

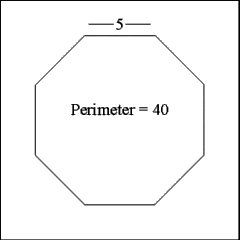
When all the construction lines are removed one is left with a regular octagon with sides 5 inches long and a perimeter of 40 inches

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~