Although many engineering manuals of the period mention the relative pointlessness of four salient stars forts it seems a good idea to understand how to construct such a thing, if only because many engineers of the period chose to ignore their own good advice and employed this trace when it seemed answer the defensive requirements of a particular position. As a matter of technical progression, star shapes were almost always founded on polygons with the same number of sides as the desired star had salients. In this example the four salient star has its origin in a four sided polygon with equal angles and equal sides: to get to the point of drawing the star it will first be necessary to construct a square. For convenience the square will have a perimeter of 48 inches and each side will be 12 inches long... knowing the length will make it much easier to produce the indentions in each side that will be necessary to convert the square into a well pointed star.

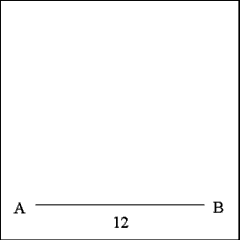
Construct a square with sides that are 12 inches long. Draw a right line AB that is 12 inches long. This will be the base construction line for the square and represents one side of the square.

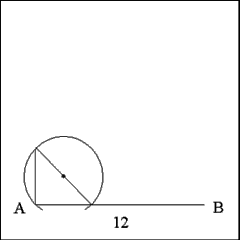
Construction the second side of the square by constructing a perpendicular line from Point A.

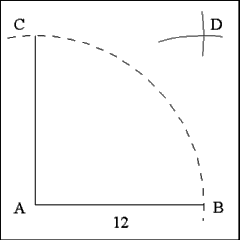
Extend the perpendicular line (AC) to a length of 12 inches; check the length by describing an arc of a circle with a radius equal to the distance between Points A and B through Point C.

Using Point C as center describe an arc of a circle with a radius of 12 inches above point B on Line AB; do the same again using Point B as center. Mark the point where the two arcs intersect as Point D.

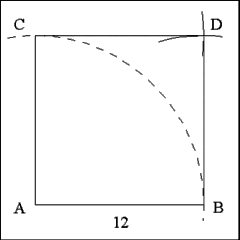
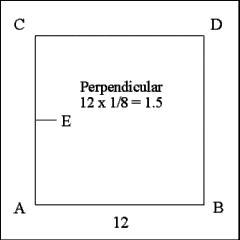
Produce right lines from Point C to Point D and from Point B to Point D. These form the third and fourth sides of the required the square ACDB.

To convert the square into a star it will be necessary to create an indention on each side of the square. This is performed by bisecting each side of the square and producing a line perpendicular to the side of the square toward the interior of the square.

The length of this perpendicular will determine the measure of the angles of the star's salients, that is how pointy they will be when the star is completed. It was a customary thing in the nineteenth century to take the perpendicular for a square as equal to one-eighth (1/8) the length of the side. In this case the sides are 12 inches, so 12 x 1/8 = 1.5; the perpendiculars will then be 1.5 inches long. The perpendicular E is then, 1.5 inches long.

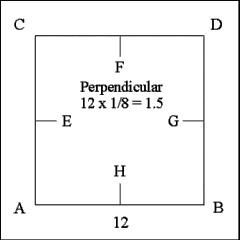
Continue the construction by bisecting each side and dropping the remaining three perpendiculars, F, G, and H. All of these lines are 1.5 inches long.

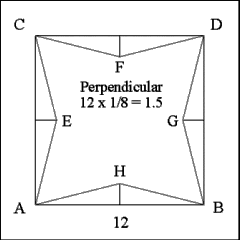
Complete the star by producing lines from each corner to the interior extremities of collateral perpendiculars; that is, from D to F and D to G, B to G and H, A to H and E, and C to E and F. These lines form the faces of the four salient angles of the four salient star.

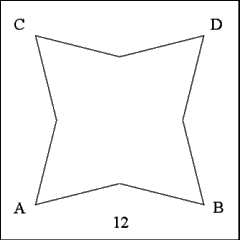
Everything clears up quite a bit when all the construction lines and marks are removed leaving, of course, the faces of the four salient star intact.

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~