|
|
|
 |
|
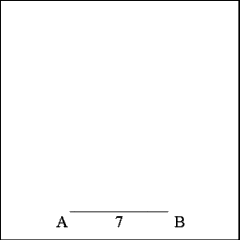
Draw a right line (AB) that will serve as the base line of the
regular pentagon. In this case Line AB should be 1/5 of the perimeter of
the pentagon or 7 inches long. |
 |
|
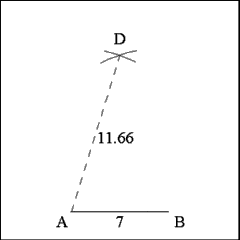
Describe two arcs of circles centered on Points A and B with radii
that are equal to one-third (1/3) the perimeter of the pentagon (35 x 1/3
= 11.66) that intersect at D. |
 |
|
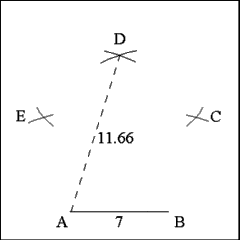
Find the vertices of the angles of the pentagon between
Point A and D and B and D by describing arcs of circles with radii equal
to the length of the side of the pentagon (7 inches) that are centered on
the three known vertices: A and D; B and D. Mark the points where the arcs
intersect as Points E and C |
 |
|
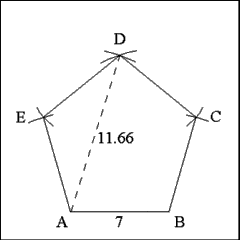
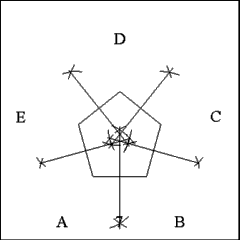
Produce right lines to connect successive vertices. These lines
form the five sides of the pentagon. All sides should be 7 inches long. |
 |
|
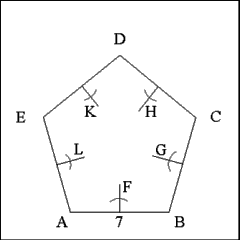
Continue to construct the five salient star by bisecting each
side of the pentagon. |
 |
|
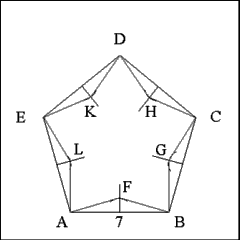
Take a distance equal to one-seventh (1/7) the side of the pentagon
on the interior of each bisecting perpendicular line. Each side of the pentagon
is 7 inches long, so 7 x 1/7 = 1. Perpendiculars K, H, G, F, and L are all
1 inch long.
Lengths of the perpendiculars determine the angular measures of
the star's five salient points; increase the length of the perpendicular
to decrease the angular measure of the salients. Length of the perpendicular
should be about one-fourth (1/4) the side to give the angles a measure of
about 60 degrees. |
 |
|
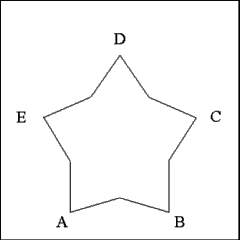
Form the sides of the five salient star by producing right lines
from each angle of the pentagon to the interior extremities of collateral
perpendiculars; D to K and H, C to H and G, B to G and F, A to F and L, and
E to L and K. |
 |
|
Erase all of the construction lines and marks to reveal the 10
sided five salient star. |
|
|
|