This construction that advantage of the properties of isosceles right triangles; when two sides of the triangle (CD and DE) are equal and angle CDE is 90 degrees, the two smaller angles (ECD and CED) will split the difference (180-90=90/2= 45) and form 45 degree angles.

Given a right line AB construct a second line that intersects Line AB at a 45 degree angle.

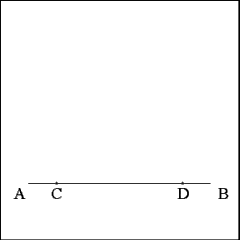
Select and mark any point (C) on Line AB that will serve as the vertex of the 45 degree angle presently under construction. Select any point (D) to construct a line perpendicular to Line AB.

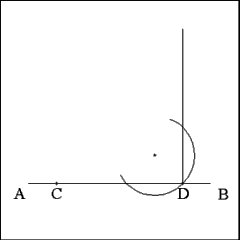
Construct a line at Point D that is perpendicular to Line AB, being mindful to extend the perpendicular somewhat beyond the estimated distance between Points C and D on Line AB.

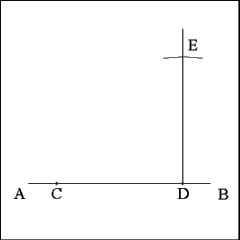
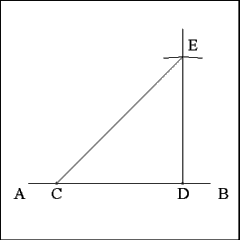
Using Point D as center cut the perpendicular with an arc of a circle that has a radius equal to the distance between Points C and D on Line AB. Line segments CD and DE should be the same length.

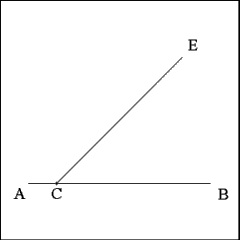
Produce a right line from Point C on line AB to Point E.

When all construction lines are removed the Angle ECB should measure 45 degrees

~ An Instructive Animation Wherein the Foregoing Construction is Visually Explained ~