 |
|
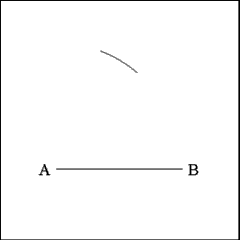
Given a right line AB that is 9 inches long begin constructing
a six salient star by first constructing a equilateral triangle.
Using Point A as center describe an arc of a circle that has a
radius equal to the length of Line AB (9 inches). |
 |
|
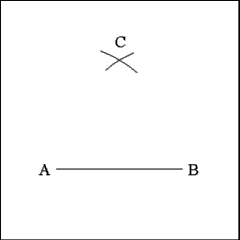
Describe a second arc with a radius equal to the length of Line
AB centered on Point B. Mark the point where this arc intersect the first
arc as Point C. |
 |
|
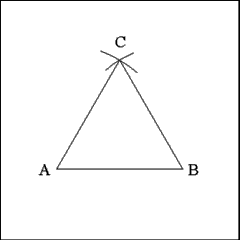
Produce right lines to connect consecutive points: A to C, C to
B. These lines form the three sides of an equilateral triangle. |
 |
|
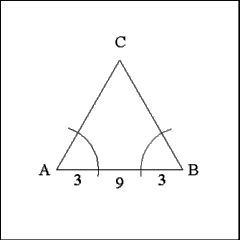
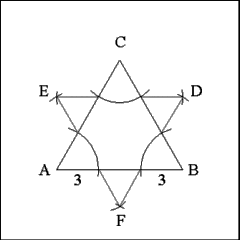
Trisect each side of the triangle into three equal segments.
Trisections can only be performed by measuring the sides (9 inches
in this case) and dividing the length by three (9/3=3). Once the third part
is known the sides can be trisected by opening the compass to the appropriate
scale length (3 inches) and using each angle as a center to describe arcs
that cut adjacent sides of the triangle. |
 |
|
Complete the six salient star by constructing equilateral triangles
on the center segment of each trisected side.
Each face of the six salient star is 1/12 the perimeter of the
star. In this example each face is 3 inches long giving the star a perimeter
of 36 inches. Each side of the original equilateral triangle is 1/3 of the
constructed star's perimeter, a proportion that is very useful to know when
the perimeter of the star is given and the exact measure of the sides of
the equilateral triangle must be determined. |
 |
|
Finally, remove all construction lines and marks to make the six
salient star look neat and clean. |
|
|
|