 |
Given an angle ABC bisect the angle into two smaller equal angles. |
|
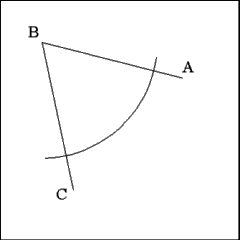 |
Using the vertex (Point B) as center describe an arc of a circle
of any radius that cuts both leg BC and leg AB. |
|
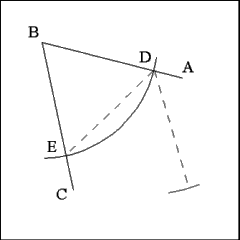 |
Marking the points where the arc cuts the legs as Point D and
Point E and using Point D as center describe an arc of a circle that has
a radius equal to the distance between Points D and E. |
|
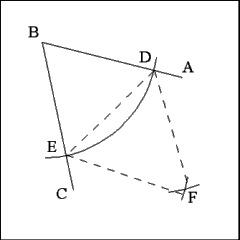 |
Using Point E as center, describe a second arc that has a radius
equal to the distance between Points D and E. Mark the point where this arc
intersects the arc centered on Point D as Point F. |
|
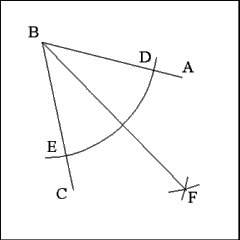 |
Using a straightedge produce a line that passes from the vertex of the angle
(Point B) through Point F. |
|
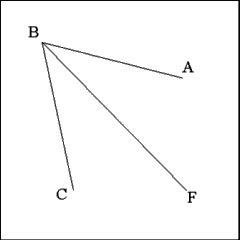 |
Line BF should bisect Angle ABC into two equal angles ABF
and FBC. |
|
|
|
|