|
This construction can be quite useful in locating the position
of accessory field work inside a larger field fortification; or in the study
of field fortifications, in testing the relative distances between ramps
leading to a parapet and the galleries of magazines or bomb-proof structures,
which says something about the general accessibility of interior works to
the fighting surfaces of a fortification. |
 |
|
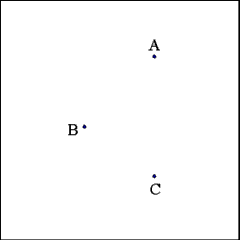
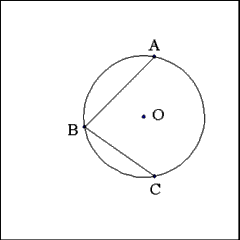
Given three widely dispersed points (A, B, and C) construct
a circle the circumference of which passes neatly through all three given
points. |
 |
|
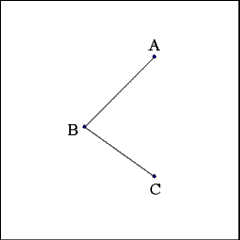
Produce two right lines that connect the three points, A to
B and B to C. |
 |
|
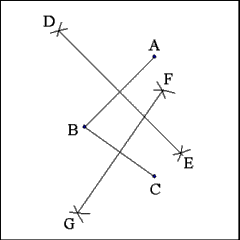
Bisect both Line AB (with Line DE) and Line BC (with Line
FG). Note that these bisecting lines (DE and FG) should intersect each other. |
 |
|
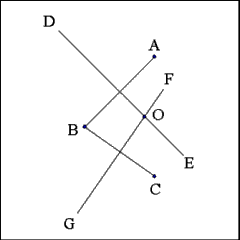
Mark the point where Line DE intersects Line FG as Point O.
This will be the center point of the required circle. |
 |
|
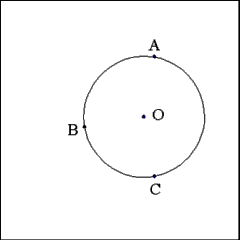
Using Point O as center describe a circle with a radius equal
to the distance between Point O and any of the three other Points (A, B,
or C). |
 |
|
All three given points should be on the circumference of Circle
O. |
|
|
|
~ An Instructive Animation Wherein the Foregoing Construction is Visually
Explained ~ |
 |
|