|
|
|
 |
|
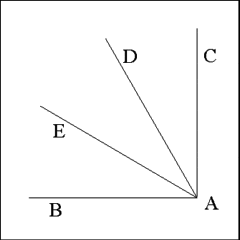
Given a right angle with its vertex at Point A trisect the angle
into three equal angles. |
 |
|
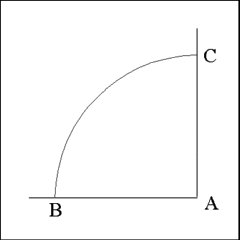
Using Point A as center describe an arc of a circle of any radius that cut
both legs of the right angle, in this case at points B and C. |
 |
|
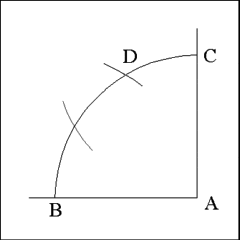
Using Point B as center describe an arc of a circle that has a radius equal
to the distance between points B and A that cuts Arc BC at Point D. Using
Point C as center, describe a second arc with a radius equal to the distance
between points A and C that cuts Arc BC. |
 |
|
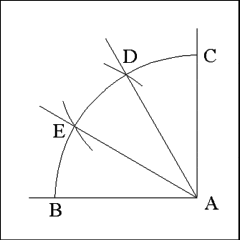
Having marked the second cut cut through Arc BC as Point E, use a straightedge
to produce right lines from Point A through, first, Point D and then through
Point E. |
 |
|
Lines AD and AE trisect the right angle into three smaller angles (BAE, EAD,
and DAC) that are equal to each other. Each angle should measure 30
degrees. |
|
|
|
|
|
|