Geometrical figures consist of the various lines and shapes capable of mathematical analysis and graphical description used and produced by abstract and practical geometry. These include polygons, circles, triangles, and their derivatives such as quadrilaterals, angles, and arcs of circles. Geometrical figures are among the most basic and most important tools required to represent any type of fortification on paper; drawing a well proportioned bastion front of fortification, for example, requires an assumption of the number of sides of the polygon of fortification which is, essentially, a geometrical figure employed to regulate the defensive relations of the various elements of the bastion front. In field fortification redoubts and other enclosed works were classified by the polygon described by the trace of their interior crests. An ability to mathematically analyze geometrical figures in terms of area and perimeter was an absolute necessity for the design and construction of most types of field works, from equalizing an intended garrison to a particular polygon with sides of a particular length to the dimensions of the flat areas required to securely mount a fortification's artillery armament on rectangular, trapezoidal, or even round platforms. In short, drawing fortifications as they were designed and constructed in the middle period of the nineteenth century requires a thorough understanding of the various geometrical figures.

The following list defines and describes various geometrical figures most likely to be encountered in drawing nineteenth century fortifications:

Angle

An angle (BAC) is formed when two lines  (AB and AC) intersect at a single point (A).

The point of intersection (A) is called the vertex of the angle. The intersecting lines (AB and AC) are called the sides (or sometimes legs) of the angle.

Angles are designated by three letters in the order: leg, vertex, leg. (BAC or CAB). They may also be designated simply by the letter of the vertex: Angle A.

Angle: Measure of an Angle

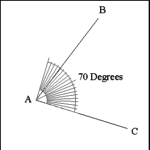
Angles are measured in degrees of an arc of a circle. Angle BAC is 70 degrees.

Angles are usually measured using a protractor.

Acute and Obtuse Angles

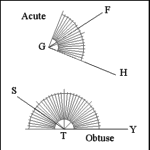
An angle is acute when its measure is less than 90 degrees. FGH is an acute angle.

An angle is obtuse when its measure is greater than 90 degrees. STY is an obtuse angle.

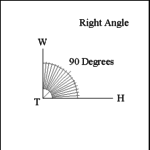
Right Angle

An angle is a right angle when it measures 90 degrees. WTH is a right angle.

When one line (WT) intersects another (TH) to form a right angle (WTH) the lines are perpendicular to each other.

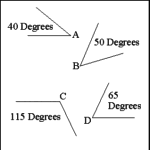
Complementary and Supplementary Angles

Two angles are complementary when the sum of their measures equals 90 degrees. Angles A and B are complementary (40 + 50 = 90).

Two angles are supplementary when the sum of their measures equals 180 degrees. Angles C and D are supplementary (115 + 65 = 180).

Triangle
Closed figure with three sides that join to form three angles.
Sum of interior angles is always 180 degrees.
Area:		A = 1/2(Base x Height)
Perimeter:		P = Sum of all sides

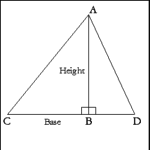
Triangle: Base and Height

Height of a triangle is measured on a line (AB) drawn perpendicular from one vertex (A) to the side the opposite vertex (CD). Height of a triangle is also called its altitude.

Base of a triangle is the side (CD) to which a perpendicular measuring the height has been drawn.

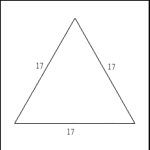
Equilateral Triangle
All three side have the same length.
Equilateral triangles are also equiangular: all three angles measure 60 degrees.

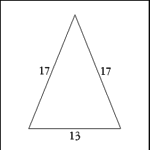
Isosceles Triangle

Two sides have equal lengths; angles opposite equal sides are also equal.

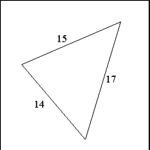
Scalene Triangle

No sides have the same length; no angles are equal.

Acute Triangle

A triangle in which the measure of each of the three angles is less than 90 degrees.

Obtuse Triangle

An obtuse triangle includes one angle that is greater than 90 degrees.

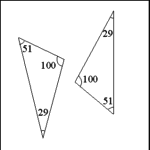
Similar Triangles

Triangles are similar when two angles of one triangle have the same measure as two angles of another triangle.

Each of the triangles in the illustration have angles that measure 100 and 51 degrees, therefore they are similar triangles.

Sides of similar triangles are proportional.

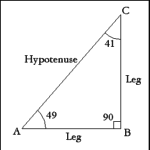
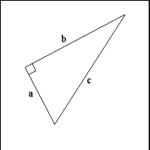
Right Triangle

A right triangle has one right (90 degree) angle (ABC).

Sides adjacent to the right angle (AB; CB) are called Legs.

Side opposite the right angle (AC) is called the Hypotenuse.

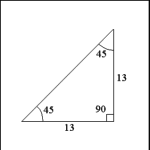
Isosceles Right Triangle

Any right triangle with legs adjacent to the right angle that are the same (equal) length.

Each angle opposite an equal side always measures 45 degrees.

Right Triangle: Pythagorean Theorem

In a right triangle the sum of the lengths of each leg squared is equal to the length of the hypotenuse squared or, mathematically stated: a2 + b2 = c2.

To find the length of c when the lengths of a and b are known: a = 4 and b=7; a2 = (4 x 4); b2 = (7 x 7): a2 = 16; b2 = 49 so 16 + 49 = 65; c2 = 65. Square root of 65 = 8.06. The hypotenuse c has a length of 8.06.

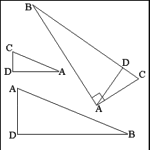
Right Triangle: Altitude and Similar Triangles

In a right triangle an altitude produced from the vertex of the right angle to the hypotenuse divides the right triangle into two similar right triangles.

The altitude AD divides right triangle BAC into two similar triangles ADC and BDA.

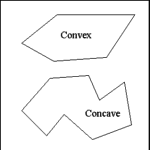
Polygon

A polygon is any figure closed by three or more right lines.

Each right line forming a polygon is called a side.

Polygons can be either convex with all angles directed toward the exterior of the figure or concave with one or more angles directed toward the interior of the figure.

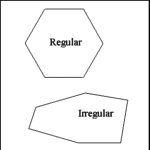
Polygons: Regular and Irregular

Polygons may be either regular or irregular.

A regular polygon has all sides the same length and all angles the same measure.

An irregular polygon does not have all sides the same length and not all angles are the same measure.

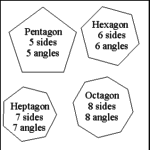
Polygons: Named by Number of Sides

Polygons are named according to the number of sides composing the closed figure. Polygons also have the same number of angles as they have sides.

Triangle: 3 sides, 3 angles; Square: 4 sides, 4 angles; Pentagon: 5 sides, 5 angles; Hexagon: 6 sides, 6 angles; Heptagon: 7 sides, 7 angles; Octagon: 8 sides, 8 angles.

Convex polygons with more than 8 sides are rarely encountered in the study of field fortifications; concave polygons with more than 8 sides (stars and irregular polygons) are quite common.

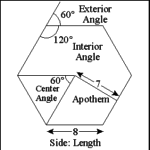
Measuring Polygons

Polygons are measured by the length of their sides and the measure of their angles in degrees of arc of a circle.

Perimeter: sum of the sides; for a regular polygon: length of one side multiplied by the number of sides; 8 x 6 = 48, the polygon in the illustration has a perimeter of 8 units.

Area of a regular polygon can be found by multiplying the sum of the length of the sides by the apothem (a perpendicular line produced from the center of the polygon to one of the sides) and multiplying the product by one-half or: Area = 1/2 (Apothem x Perimeter). In this case (7 x 48) x 1/2 = 168 square units (approximately, since the apothem was rounded).

Interior angles of regular polygons may be found by subtracting 2 from the number of sides and multiplying the result by 180 degrees. This gives the sum of the interior angles; the measure of each interior angle can be found by dividing the sum of the interior angles by the number of sides. The regular hexagon in the illustration would be calculated: (6 - 2) x 180 = 720 (sum of the interior angles); each angle: 720 ÷ 6 = 120. So each interior angle has a measure of 120 degrees.

Sum of the exterior angles of a regular polygon is found by dividing 360 by the number of angles; in this case 360 ÷ 6 = 60. This formula can also be used to find the angular measure of a regular polygon's central (or center) angle.

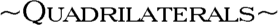Quadrilateral Polygons

Quadrilaterals are polygons that have four sides and four angles.

This special category of polygon includes: Square, Parallelogram, Rhombus, Rectangle, and Trapezoid.

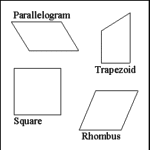
Quadrilateral: Square

A square is a quadrilateral polygon in which all four sides have equal lengths, opposite sides are parallel, and all four angles are right angles (90 degrees).

Perimeter: Multiply the length of one side by four: P = 4(S). In the example: 4 x 13 = 52. The square has a perimeter of 52 units.

Area: Multiple one side by another side (or, the base by the height): A = S1(S2). In the example: 13 x 13 = 169. The square has an area of 169 square units.

Two diagonals produced across a square will be perpendicular to each other. A single diagonal will divide a square into two similar isosceles right triangles. Length of a diagonal line drawn through a square will have a ratio of 1.414  to 1 or be approximately 10/7 the length of the side of the square. In the example the diagonal will be 1.414 x 13 = 18.38 units long.

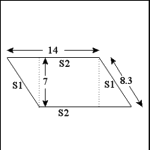
Quadrilateral: Parallelogram

A parallelogram is a four sided polygon in which opposite sides are parallel and its angles are not right angles.* In the illustration sides marked S1 are parallel to each other and sides marked S2 are parallel to each other.

Perimeter: Add the length of one of each parallel sides and multiply the sum by 2: P = 2(S1 + S2). In the example: (8.3 + 14) x 2 = 44.6. The perimeter of the parallelogram is 44.6 units.

Area: Multiply the Base by the Height: A = BH. In the example: 14 x 7 = 98. The area of the parallelogram is 98 square units.

* Modern works on geometry allow the angles of a parallelogram to be right angles; some nineteenth century works on practical geometry particularized a sub-type of parallelograms by requiring the angles to not be right angles and denominated them rhomboids.

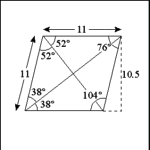
Quadrilateral: Rhombus

A rhombus is a quadrilateral polygon in which all four sides are the same length and opposite sides are parallel. When a rhombus' angles are not right angles this figure is sometimes referred to as a lozenge.

Perimeter: The perimeter of a rhombus is found by multiplying one side by four: P = 4(S). In the example: 4 x 11 = 44. The rhombus has a perimeter of 44 units.

Area: Area of a rhombus is found by multiplying the base by the height: A = BH. In the example: 11 x 10.5 = 115.5. The area of the rhombus is 115.5 square units.

Diagonals produced to opposite angles bisect those angles; two diagonals produced across a rhombus are perpendicular to each other. Collateral angles are supplementary.

Quadrilateral: Trapezoid

A trapezoid is a quadrilateral polygon in which two opposite sides are parallel and two opposite sides are not parallel.

Perimeter: The perimeter of a trapezoid is found by adding the lengths of all four sides: P = S1 + S2 + S3 + S4. In the example: 15 + 12 + 12 + 11.6 = 50.6. The perimeter of the trapezoid is 50.6 units.

Area: The area of a trapezoid can be found by adding the lengths of the two parallel sides, multiplying the sum by 1/2 and then multiplying the product by the distance between the two parallel sides (or base): A = 1/2(S1 + S2)B. In the example: 15 + 12 = 27; 27 x 1/2 = 13.5; 13.5 x 11.6 = 156.6. The trapezoid has an area of 156.6 square units.

Note:  Typical representations of trapezoids show opposite sides that are not parallel as being inclined, with the shorter parallel side at the top. In the study of field fortifications trapezoids are usually encountered in the form shown in the first illustration, with just one side being inclined. The typical form is usually encountered when dealing with artillery platforms, cross-sections of traverses, and field powder magazines.

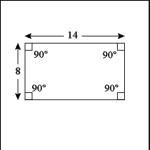
Quadrilateral: Rectangle

A rectangle is a quadrilateral polygon in which opposite sides are parallel and all angles are right angles. Opposite sides are the same length.

Perimeter: Perimeter of a rectangle is found by multiplying one of each of the parallel sides by two and adding the products, the sum is the perimeter: P = 2(S1) + 2(S2). In the example: (8 x 2) + (14 x 2) = 16 + 28 = 44. The perimeter of the rectangle is 44 units.

Area: Area of a rectangle is found by multiplying the length of one of two parallel sides (base) by the length of one of the other parallel sides (height): A = BH. In the example: 8 x 14 = 112. The rectangle has an area of 112 square units.

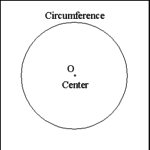
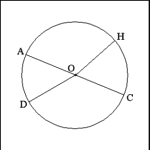
Circle

A circle is a figure closed by a curved line that has all its points throughout its length equidistant from a single point. The enclosing curved line is called the circumference of the circle; the point that all points of the circumference are equally distant from is called the center of the circle.

Circles are usually designated by a letter assigned to their center point. The circle in the illustration is Circle O.

Circle: Diameter and Radius

A diameter of a circle is a right line produced from any point on the circumference of the circle that passes through the center point of the circle and terminates on the circumference of the circle. Line AC that passes through Center Point O is a diameter of Circle O.

In all circles the ratio of the length of the circumference to the length of the diameter is 3.14 to 1 (3.14:1). The circumference will be 3.14 times longer than the diameter.

A radius of a circle is a right line produced from the center point of the circle to any point on the circumference of the circle. Line OD and Line OH are radii of Circle O.

Note that the lines traced from Point D to Center Point O to Point H are not a diameter since they form an angle (DOH) and do not constitute a single right line.

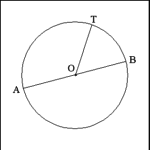
Circle: Perimeter and Area

Perimeter: The perimeter, or more appropriately, the circumference, of a circle is found by multiplying the length of the diameter by 3.14 (also called Pi or, symbolically: ). If the diameter AB = 26, then the circumference is calculated: C = 26 x 3.14; C = 81.64 units. The circumference is 81.64 units long.

Area: The area of a circle is found by multiplying 3.14 (Pi) by the length of the radius squared (that is, multiplied by itself): A = 3.14(r2). In the example, if the radius OT = 12, then A = 3.14 x (12 x 12); A = 452.16. The circle has an area of 452.16 square units.

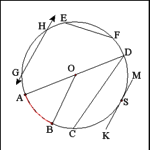
Circle: Arcs, Lines, Angles, and Points Defined

Arc of a Circle: An Arc of a circle is portion of the circumference of a circle. The portion from A to B is an arc of Circle O.

Central or Center Angle: An angle within a circle that has its vertex at the center point of the circle. Angle AOB is a center angle of Circle O.

Angle of the Circumference (or, Inscribed Angle): An angle within a circle that has its vertex on the circumference of the circle and legs that terminate on the circumference. Angle ADC is an angle of the circumference. An angle of the circumference has an angular measure that is one-half the degree measure of the arc formed by the intersection of its sides with the circumference: the measure of Angle ADC is one-half the degree measure of Arc AC.

Chord of a Circle: A Chord of a circle is any line produced from one point on the circumference to another point on the circumference: Line EF, Line AD, and Line CD are chords of Circle O.

Secant: A secant is a line that passes through two point of the circumference of a circle and whose end points are outside the circumference of the circle. Line GH is a secant of Circle O.

Tangent: A tangent is a line that intersects the circumference of the circle at one (and only one) point. The point of intersection is called the point of tangency. Line KM is tangent to Circle O with the point of tangency at Point S.

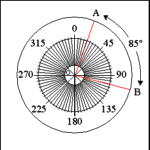
Circle: Measuring Angles with Circle Arcs

By convention circles are divided into 360 equal parts called degrees; each degree is divided into 60 equal parts called minutes and minutes are in turn divided into 60 equal parts called seconds.

Degrees of a circle are used to measure the width of the opening between the sides of angles. This is called a degree measure as opposed to a measure of length (distance) or volume.

In the example circle to the left, a smaller circle divided into 5 degree units has been superimposed in Circle O and the number of degrees of the circle marked for every 45 degrees around the circle (45, 90, 135, etc...). All circles, no matter how large or small, are divided into 360 degrees; the smaller circle and Circle O have the same number of degrees.

The opening of center angle AOB measures 85 degrees from side OA to side OB along the arc AB on the circumference of Circle O.

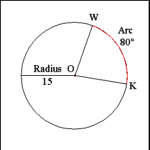
Determining the Length of an Arc of a Circle

To determine the length of an arc of a circle multiply the number of degrees in the arc by 3.14 (pi) by the length of the radius of the circle and divide the product by 180.

Determine the length of Arc WK: 80 x 3.14 x 15 = 3768; 3768 ÷ 180 = 20.93. Arc WK is 20.93 units in length.

Current Version: February, 2007